| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- DynamicProgramming
- tensorflow
- 강의자료
- Cross entropy
- 딥러닝
- loss
- 홍콩과기대김성훈교수
- Hypothesis
- 백준
- Python
- pytorch
- Deep learning
- Natural Language Processing with PyTorch
- 정렬
- machine learning
- DP
- classifier
- 파이토치
- AI
- 머신러닝 기초
- 강의정리
- 머신러닝
- BAEKJOON
- rnn
- MSE
- 파이썬
- 알고리즘
- 자연어처리
- 스택
- Softmax
- Today
- Total
개발자의시작
Natural Language Processing with PyTorch 정리 3-1 본문
이 글은 Natural Language Processing with Pytorch 강의자료를 번역 및 정리해놓은 글입니다.
강의 자료 및 코드 링크 :
dlsucomet/MLResources
Repository for Machine Learning resources, frameworks, and projects. Managed by the DLSU Machine Learning Group. - dlsucomet/MLResources
github.com
이 장에서는 활성화 함수, 손실 함수, 옵티마이저 및 지도 학습 설정과 같은 신경망 구축과 관련된 기본 아이디어를 소개한다. 신경망 하나의 단위인 퍼셉트론(perceptron)을 살펴보면서 다양한 개념을 하나로 묶는다.
퍼셉트론 자체는 보다 복잡한 신경망의 빌딩 블록이다. 여기서 소개하는 모든 아키텍처 또는 네트워크는 독립형 도는 다른 복잡한 네트워크 내에서 구성적으로 사용될 수 있으며, 책 전반에 걸쳐 반복되는 일반적인 패턴이다.
The Perceptron: The Simplest Neural Network
가장 간단한 신경망 유닛은 퍼셉트론(perceptron)이다. 퍼셉트론은 역사적으로 생물학적 뉴런 이후 매우 느슨하게 모델링 되었다. 생물학적 뉴런과 마찬가지로 입력과 출력이 있으며, "신호"(signal)은 그림 3-1과 같이 입력에서 출력으로 전해지게 된다.

각 퍼셉트론 장치에는 입력(x), 출력(y) 및 3개의 "knobs"(일종의 함수 또는 연산)가 있다. "knobs" : 가중치 세트(w), 바이어스(b) 및 활성화 함수(f). 가중치와 바이어스는 데이터를 통해 학습되며, 네트워크 디자이너의(프로그래머)의 네트워크 직감 및 목표 출력에 따라 활성화 함수가 직접 선택된다. 이를 수식으로 표현하면 다음과 같다.
y = f ( wx + b )
일반적으로 퍼셉트론에는 하나 이상의 입력이 있다. 벡터(vectors)를 사용하여 이 일반적인 경우를 표현할 수 있다. 즉, x와 w는 벡터이고 w와 x의 곱은 내적으로 대체되어 표현된다.
여기서 f로 표시된 활성화 함수는 일반적으로 비선형 함수이다. 선형 함수는 그래프가 직선으로 이루어진 함수이다. 위에서 본 예인 wx + b 는 선형 함수이다. 따라서 본질적으로 선형 및 비선형 함수의 구성이다. 선형 표현인 wx + b는 "affine transform"이라고도 한다.
아래의 example 3-1에서 Pytorch로 구현된 퍼셉트론을 제시하여, 임의의 수를 입력받아 선형변환"affine transform"을 수행하고, 활성화 함수를 적용하여, 단일 출력을 생성하는 것을 보인다.
example 3-1. Implementing a perceptron using PyTorch
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
import torch
import torch.nn as nn
class Perceptron(nn.Module):
""" A perceptron is one linear layer """
def __init__(self, input_dim):
"""
Args:
input_dim (int): size of the input features
"""
super(Perceptron, self).__init__()
self.fc1 = nn.Linear(input_dim, 1)
def forward(self, x_in):
"""The forward pass of the perceptron
Args:
x_in (torch.Tensor): an input data tensor
x_in.shape should be (batch, num_features)
Returns:
the resulting tensor. tensor.shape should be (batch,).
"""
return torch.sigmoid(self.fc1(x_in)).squeeze()
|
cs |
PyTorch는 torch.nn 모듈에 편리하게 선형 클래스를 제공하여 가중치 및 바이어스에 필요한 부기를 유지하고 필요한 선형 변환을 수행합니다. 뒤에 "Diving Deep into Supervised Training"에서는 데이터에서 가중치 w 및 b의 값을 "학습(learn)" 하는 방법을 설명한다. example 3-1)에서 사용된 활성화 함수는 Sigmoid 함수이다. 다음 섹션에서 Sigmoid함수와 함께 몇 가지 일반적으로 사용하는 활성화 함수를 살펴본다.
Activation Functions
활성화 함수(activation function)는 데이터의 복잡한 관계를 포착하기 위해 신경망에 도입된 비선형성이다. "Diving Deep into Supervised Training"과 다층 신경망(multilayer perceptron)은 왜 학습에 비선형성이 필요한지에 대해 자세히 설명하고, 먼저 일반적으로 사용되는 몇 가지 활성화 함수를 살펴본다.
Sigmoid
Sigmoid 함수는 신경망 역사에서 가장 초기에 사용된 활성화 함수 중 하나이다. 실제 값을 취하여 0에서 1 사이의 범위로 "찌그러뜨린다"(책에서는 찌그러뜨린다는 표현을 사용하였는데, 이는 실수를 0~1 사이의 값으로 매핑한다는 의미).
수학적으로 sigmoid 함수는 다음과 같이 표현된다.

example 3-2. Sigmoid activation
|
1
2
3
4
5
6
|
import torch
import matplotlib.pyplot as plt
x = torch.range(-5.,5., 0.1)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
|
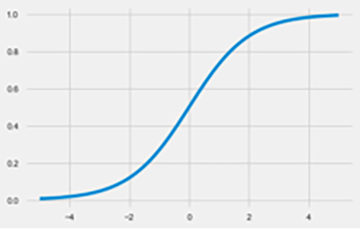
플롯에서 볼 수 있듯이, sigmoid 함수는 대부분의 입력에 대해 매우 신속하게 포화됩니다 (즉, 극한값의 출력을 생성함). 그래디언트가 0이 되거나 오버플로 부동 소수점 값으로 분기될 수 있으므로 문제가 될 수 있다. 이러한 현상은 각각 소실 구배 문제 및 폭발 구배 문제라 고도한다. 결과적으로 출력 이외의 신경망에서 사용되는 시그 모이 드 단위를 보는 경우는 드물며, "스쿼싱" 속성으로 출력을 확률로 해석할 수 있다.
Tanh
Tanh 활성화 기능은 sigmoid의 외관상 다른 변형이다. tanh에 대한 표현식을 작성할 때 이것은 분명해집니다.

예제 3-3) 에 표시된 것처럼 tanh가 단순히 sigmoid 함수의 선형 변환임을 확신할 수 있다. 또한 tanh ()에 대한 PyTorch 코드를 작성하고 곡선을 그릴 때도 분명하다. sigmoid와 같이 tanh도 "스쿼싱"함수입니다. 단, 실제 값 세트를 (–∞, + ∞)에서 [1, +1]로 매핑한다.
example 3-2. Tanh activation
|
1
2
3
4
5
6
7
|
import torch
import matplotlib.pyplot as plt
x = torch.range(5.,5., 0.1)
y = torch.tanh(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
|

ReLU
ReLU 정류 선형(rectified linear) 단위를 나타낸다. 이것은 아마도 가장 중요한 활성화 함수이다. 실제로 ReLU를 사용하지 않으면 딥 러닝의 최신 혁신 중 상당수가 불가능했을 것이라고 말할 수 있다. sigmoid와 Tanh는 -1~1 사이의 값들을 반환하므로 가중치가 곱해지면 작아질 수밖에 없는 구조이다. 출력 결과의 차이를 0에 가까운 작은 차이를 비교하는 것보다 큰 값으로 비교하는 것이 그 차이를 파악하고 계산하는데 유리하다. 이것을 가능하게 하는 것이 ReLU이며 표현식은 아래와 같다.

ReLU가 수행하는 작업은 음수 값은 모두 0으로 잘라버린다.
example 3-2. ReLU activation
|
1
2
3
4
5
6
7
|
import torch
import matplotlib.pyplot as plt
relu = torch.nn.ReLU()
x = torch.range(5.,5., 0.1)
y = relu(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
|

기울기 소멸 문제를 도와주는 ReLU의 클리핑(clipping) 효과도 문제가 될 수 있다. 시간이 지남에 따라 네트워크의 특정 출력이 단순히 zero가 되어 다시는 어떤 값을 곱해도 살아날 수가 없다. 이것을 'dying ReLU"문제라고 한다. 이러한 영향을 완화하기 위해 누출 계수 a가 학습된 매개 변수 및 Leaky ReLU 활성화 함수 같은 변형이 제안되었다.
example 3-2. ReLU activation
|
1
2
3
4
5
6
7
|
import torch
import matplotlib.pyplot as plt
prelu = torch.nn.PReLU(num_parameters=1)
x = torch.range(5.,5., 0.1)
y = prelu(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
|

Softmax
활성화 함수의 또 다른 선택은 Softmax이다. sigmoid 함수와 마찬가지로 softmax 함수는 example 3-6에 보이는 바와 같이 각 장치의 출력을 0과 1 사이로 "찌그러 뜨린다". 그러나 softmax 연산은 각 출력을 모든 출력의 합으로 나눈다. 이는 k개의 가능한 클래스에 대한 이산 확률 분포를 제공한다.

결과 분포의 확률을 모두 더하면 1이다. 이것은 분류 작업에 대한 결과를 해석하는데 매우 유용하므로 이 변환은 일반적으로 categorical croos entropy와 같은 확률적 학습 목표와 쌍을 이룬다("Diving Deep into Supervised Training"에서 자세하게 다룸")
example 3-6. Softmax activation
|
1
2
3
4
5
6
7
8
|
import torch.nn as nn
import torch
softmax = nn.Softmax(dim=1)
x_input = torch.randn(1, 3)
y_output = softmax(x_input)
print(x_input)
print(y_output)
print(torch.sum(y_output, dim=1))
|
출력 결과
|
1
2
3
|
tensor([[ 0.5836, 1.3749, 1.1229]])
tensor([[ 0.7561, 0.1067, 0.1372]])
tensor([ 1.])
|
이 섹션에서는 4가지 중요한 활성화 함수인 sigmoid, Tanh, ReLU, softmax를 살펴봤다. 이것은 신경망을 구축하는 데 사용할 수 있는 네 가지에 불과하다. 이 자료를 진행하면서 어떤 활성화 함수를 사용해야 하고 어디에 사용하는지 명확하게 알 수 있지만, 일반적인 방법은 과거에 작동했던 것을 단순히 따라 하는 것이다.
Loss Functions
손실 함수(Loss function)는 실제 (y)와 예측(y^)을 입력으로 사용하여 실수 값의 점수를 생성한다. 이 점수가 높을수록 모델의 예측이 나빠진다. PyTorch는 여기서 다룰 수 있는 것보다 더 많은 손실 함수를 nn 패키지로 구현하지만, 가장 일반적으로 사용되는 손실 함수를 검토한다.
Mean Squared Error Loss
네트워크의 출력(y^)과 목푯(y)가 연속적인 값인 회귀 문제의 경우 일반적인 손실 함수 중 하나는 오차 평균 제곱(MSE)이다.

MSE는 단순히 예측값과 목표 값의 차이의 제곱 평균이다. 평균 절대 오차 (MAE) 및 근 평균 제곱 오차 (RMSE)와 같이 회귀 문제에 사용할 수 있는 다른 손실 함수가 몇 가지 있지만 모두 출력과 목표 사이의 실제 거리 계산과 관련이 있다. 예제 3-7에서는 PyTorch를 사용하여 MSE 손실을 구현하는 방법을 보여준다.
example 3-7. MSE loss
|
1
2
3
4
5
6
7
|
import torch
import torch.nn as nn
mse_loss = nn.MSELoss()
outputs = torch.randn(3, 5, requires_grad=True)
targets = torch.randn(3, 5)
loss = mse_loss(outputs, targets)
print(loss)
|
출력 결과
|
1
|
tensor(3.8618)
|
Categorical Cross-Entropy Loss
교차 엔트로피(categorical Cross-Entropy loss)는 일반적으로 출력이 클래스 멤버쉽 확률의 예측으로 해석되는 멀티 클래스 분류 설정에서 사용된다. 목표 (y)는 모든 클래스에 대한 실제 값의 다항식 분포를 나타내는 n개의 요소로 구성된 벡터이다. 하나의 클래스만 올바른 경우 이 벡터는 one-hot이다. 네트워크의 출력(y^)은 n개의 요소로 구성된 벡터이지만 네트워크의 다항 분포에 대한 예측을 나타낸다. categorical Cross-Entropy는 이 두 벡터 (y, y^)를 비교하여 손실을 측정한다.

교차 엔트로피와 그것의 표현은 정보 이론에서 유래하지만, 이 섹션의 목적 상, 이것을 두 분포가 어떻게 다른지 계산하는 방법으로 고려하는 것이 도움이 된다. 올바른 클래스의 확률은 1에 가깝고 다른 클래스의 확률은 0에 가깝다.
PyTorch의 CrossEntropyLoss () 함수를 올바르게 사용하려면 네트워크 출력, 손실 함수 계산 방법 및 실제로 부동 소수점 숫자를 나타내는 데 따른 계산 제약 조건의 관계를 이해해야 한다. 특히, 네트워크 출력과 손실 기능 사이의 미묘한 관계를 결정하는 4 가지 정보가 있다.
첫째, 숫자가 얼마나 작거나 클 수 있는지에 대한 제한이 있습니다. 둘째, softmax 공식에 사용된 지수 함수에 대한 입력이 음수이면 결과는 지수 적으로 작은 수이고, 양수이면 결과는 지수 적으로 큰 수이다. 다음으로, 네트워크의 출력은 softmax 기능을 적용하기 직전에 벡터로 가정된다. 마지막으로, 로그 함수는 지수 함수의 역수이며 log (exp (x))는 x와 같다. 이 네 가지 정보를 바탕으로 softmax 함수의 핵심 인 지수 함수와 더 큰 수치 적으로 안정되고 실제로 작은 숫자 나 큰 숫자를 피하기 위해 교차 엔트로피 계산에 사용되는 로그 함수를 가정하여 수학 단순화가 이루어진다.
이러한 단순화의 결과는 네트워크 출력 없이 PyTorch의 CrossEntropyLoss ()와 함께 softmax 함수를 사용하여 확률 분포를 최적화할 수 있다. 그 후, 네트워크가 훈련되었을 때, 소프트 맥스 함수는 예 38에 보인 바와 같이 확률 분포를 생성하는 데 사용될 수 있다.
example 3-8. Cross-entropy loss
|
1
2
3
4
5
6
7
|
import torch
import torch.nn as nn
ce_loss = nn.CrossEntropyLoss()
outputs = torch.randn(3, 5, requires_grad=True)
targets = torch.tensor([1, 0, 3], dtype=torch.int64)
loss = ce_loss(outputs, targets)
print(loss)
|
출력 결과
|
1
|
tensor(2.7256)
|
이 코드 예제에서는 임의의 값으로 구성된 벡터가 먼저 네트워크 출력을 시뮬레이션하는 데 사용된다. 그런 다음 PyTorch의 CrossEntropyLoss () 구현에서는 각 입력에 하나의 특정 클래스가 있고 각 클래스에 고유 한 인덱스가 있다고 가정하므로 대상이라고 하는 목표 벡터는 정수 벡터로 생성됩니다. 이것이 목표에 세 가지 요소가 있는 이유이다. 각 입력에 대한 올바른 클래스를 나타내는 색인입니다. 이 가정을 통해 모델 출력에 대한 계산 작업을 보다 효율적으로 수행할 수 있다.
Binary Cross-Entropy Loss
범주형 교차 엔트로피(Categorical Cross-Entropy Loss)는 여러 클래스가 있을 때 분류 문제에 매우 유용하다. 때로는 이진 분류라고도 하는 두 클래스를 구별하는 작업이 필요하다. 이러한 상황에서는 이진 교차 엔트로피(binaryCross-Entropy) 사용하는 것이 필요하다. 특정 상황에서 BCE 솔실 함수를 사용하는 것이 효율적이다. 이 자료에서는 "식당 리뷰의 감정 분류하기"에서 이 손실 함수를 살펴본다.
example 3-9에서, 네트워크의 출력을 나타내는 임의의 벡터에 sigmoid 활성화 함수를 사용하여 이진 확률 출력 벡터, 확률을 만듭니다. 다음으로, 실제 값은 0과 1의 벡터로 인스턴스화 됩니다. 마지막으로, 이진 확률 벡터와 실제 값 벡터를 사용하여 이진 교차 엔트로피 손실을 계산한다.
example 3-9. Binary cross-entropy loss
|
1
2
3
4
5
6
7
|
bce_loss = nn.BCELoss()
sigmoid = nn.Sigmoid()
probabilities = sigmoid(torch.randn(4, 1, requires_grad=True))
targets = torch.tensor([1, 0, 1, 0], dtype=torch.float32).view(4, 1)
loss = bce_loss(probabilities, targets)
print(probabilities)
print(loss)
|
출력 결과
|
1
2
3
4
5
|
tensor([[ 0.1625],
[ 0.5546],
[ 0.6596],
[ 0.4284]])
tensor(0.9003)
|
'자연어처리' 카테고리의 다른 글
| Natural Language Processing with PyTorch 정리 3-4 (0) | 2020.06.17 |
|---|---|
| Natural Language Processing with PyTorch 정리 3-3 (0) | 2020.06.10 |
| Natural Language Processing with PyTorch 정리 3-2 (0) | 2020.05.13 |
| [정보검색] 역색인파일(inverted index file) 정리 (0) | 2020.04.14 |
| Python 한국어 맞춤법 검사기 py-hanspell 라이브러리 사용법 (7) | 2020.04.07 |




