| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- tensorflow
- AI
- pytorch
- DP
- Softmax
- Cross entropy
- Hypothesis
- 자연어처리
- MSE
- 딥러닝
- 파이썬
- 파이토치
- 백준
- 정렬
- DynamicProgramming
- classifier
- loss
- 머신러닝 기초
- rnn
- 강의자료
- Natural Language Processing with PyTorch
- 홍콩과기대김성훈교수
- Python
- machine learning
- 스택
- BAEKJOON
- 강의정리
- Deep learning
- 머신러닝
- 알고리즘
- Today
- Total
개발자의시작
[머신러닝][딥러닝] Linear Regression의 cost 최소화 minimize cost 3.0 본문
[머신러닝][딥러닝] Linear Regression의 cost 최소화 minimize cost 3.0
LNLP 2020. 4. 23. 15:57이 글은 홍콩과기대 김성훈 교수님의 강의를 개인적으로 정리한 글입니다.
강의 영상 및 강의자료는 아래의 링크에서 확인하실 수 있습니다.
링크 : http://hunkim.github.io/ml/
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io
Hypothesis and cost
이전 포스팅에서 hypothesis와 cost를 다음과 같이 정의하였다.


편의를 위해 아래와 같이 표현할 수 있다.


데이터가 주어질때 Hypothesis의 W와 Cost는 다음과 같이 계산할 수 있다.
| X | Y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
W=1, cost(W)=0
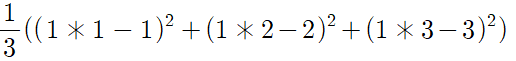
W=0, cost(W)=4.67

W=2, cost(W)=4.67

Cost function을 그래프로 나타내면 아래와 같은 그림을 그릴 수 있다.

목표는 오차(cost)를 최소로 하는 값(W)를 찾는 것이다.
오차를 최소로하는 지점을 찾는 방법으로 경사 하강법(Gradient descent)을 사용할 수 있다.
Gradient descent algorithm
경사도(기울기)를 따라서 이동하여 경사도(기울기)가 0이되는 지점을 찾아간다.
- 어느지점에서나 시작할 수 있다. ( -3 ~ 5 )
- 경사도(기울기)가 낮은 지점으로 이동할수록 오차(cost)가 줄어든다.
어떻게 경사도(기울기)를 구하는가?? -> 미분을 사용한다.
- 수식
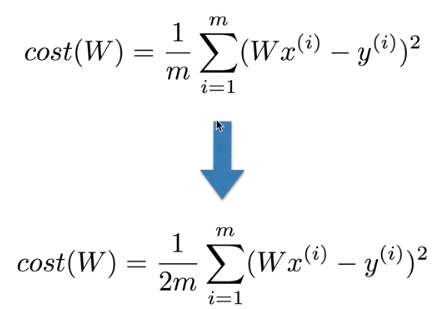
여기서 분모에 2가 곱해지는데 이는 미분을 할때 편의상 곱해주는 것.
원하는 값을 구하는데 영향을 주지 않는다.
오차를 최소로하는 W를 구하는 공식!

여기서 ∂ 는 학습률(learning rate)을 최적의 W를 찾아가는 과정에서 이동하는 정도를 의미한다.

수식을 적용하면 1 지점의 경우 기울기가 음의 값이 나오기 때문에 W의 값은 증가하게 된다.
2 지점의 경우 기울기가 양의 값이 나오기 때문에 W의 값이 감소하게 된다.
수식에 미분을 적용하는 과정은 아래와 같은 수식으로 표현할 수 있다.
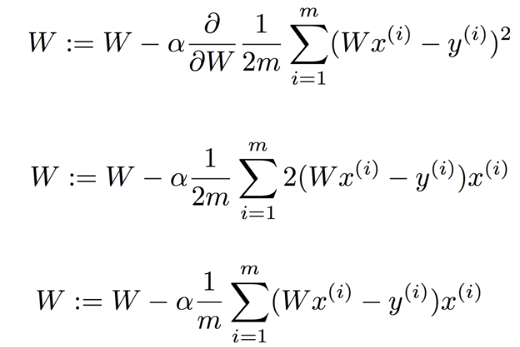
Gradient descent algorithm을 사용할 때는 주의할 점이 있다.
- 국소최적해(local minima)에 빠질 위험이 있다.

시작점의 위치에 따라 최종 도할하는 값이 달라질 수 있다.
Convex function

Gradient descent algorithm을 사용할 때는 위와 같이 어느 지점에서 시작해도 최소점에 도달할 수 있어야 한다. 위와 같은 형태의 함수를 convex function라고 하며, cost function을 설계할 때 convex function이 되도록 해야 한다.
오류 또는 이상한 점 있다면 댓글로 남겨주시기 바랍니다.
감사합니다.
'머신러닝(machine learning)' 카테고리의 다른 글
| [Pytorch] 01-1 Tensor Manipulation 1 (0) | 2021.11.26 |
|---|---|
| 도커[Docker] Instruction (0) | 2021.11.18 |
| [머신러닝][딥러닝] TensorFlow로 간단한 linear regression 구현 2.1 (0) | 2020.04.08 |
| [머신러닝][딥러닝] Linear Regression(선형 회귀)의 Hypothesis 와 cost 2.0 (0) | 2020.04.08 |
| [머신러닝][딥러닝] 에이다부스트(Adaboost) 개념 정리 (0) | 2020.04.08 |




