| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- DynamicProgramming
- 알고리즘
- Cross entropy
- 강의정리
- BAEKJOON
- classifier
- tensorflow
- Python
- 정렬
- machine learning
- rnn
- 파이토치
- Deep learning
- Natural Language Processing with PyTorch
- 백준
- 강의자료
- Hypothesis
- AI
- pytorch
- 홍콩과기대김성훈교수
- 딥러닝
- Softmax
- MSE
- 파이썬
- 자연어처리
- DP
- 머신러닝
- 스택
- 머신러닝 기초
- loss
- Today
- Total
개발자의시작
[Pytorch] 07-1 Tips 본문
글은 모두를위한딥러닝 시즌2 https://github.com/deeplearningzerotoall/PyTorch 을 정리한 글입니다.
GitHub - deeplearningzerotoall/PyTorch: Deep Learning Zero to All - Pytorch
Deep Learning Zero to All - Pytorch. Contribute to deeplearningzerotoall/PyTorch development by creating an account on GitHub.
github.com
이번 시간에 다룰 주제는 다음과 같다.
Reminder: Maximum Likelihood Estimation
Reminder: Optimization via Gradient Descent
Reminder: Overfitting and Regualarization
Training and Test Dataset
Learing Rate
Data Preprocessing
Maximum Likelihood Estimation (MLE) - 최대 우도 추정

압정이 하나 있다고 가정한다. 압정을 던져보면 땅에 떨어진 케이스는 두 가지가 있다. 납작한 부분이 땅에 붙은 경우(class 1)와 그 외의 경우(class 2)가 있다. 압정을 바닥에 던졌을 때 압정이 class 1 상태가 될지 class 2 상태가 될지 궁금하다. 즉, 확률을 알고 싶다. 분명히 압정이 어디로 떨어질지 확률 분포가 존재할 것이다. 그래서 우리는 이것을 machine learing을 통해 예측해보고 싶다. 지금은 예측해야 하는 값이 class 1과 class 2로 두 가지가 있다. 따라서 베르누이 분포(이항 분포)가 된다. 이것은 즉, 0과 1을 구분하는 Binary Classification을 수행하면 된다. binomial distribution을 구하기 위해 압정을 던져보면, 100번을 던졌을 때 class 1이 나올 확률(k)이 27번이라고 가정한다.

문제를 살펴보고 Binomial dstribution 인 것을 알았다. Binomial dstribution의 공식은 위와 같다. n이 100이었고 k는 27이라는 관측치(observation)를 갖고 있다. 수식에 각각의 값을 넣어본다. θ는 모른다. 우리가 알고 싶은 것이 바로 θ이다. θ는 압정의 확률 분포를 결정하는 파라미터 값이다. 이것이 neural network가 될 수 도 있고 지금은 단순히 binomial distribution에서 결정하는 값이 될 수 있다(이것이 만약 연속적인 값을 갖는 가우시안 분포를 따랐다면 θ는 μ 혹은 σ가 될 수도 있다).
우리는 이 공식에 따라서 어떤 함수를 만들 수 있다. 즉 θ에 대한 함수 f(θ)를 만들 수 있다. θ가 얼마일 때 n이 100이고 k가 27일 때의 값을 계산해 보면 f(θ)를 구할 수 있다. θ에 따라서 어떤 함수 θ의 함수를 구할 수 있다.

실제로 위의 수식을 그래프로 그려보면 위의 그래프와 같다. x축이 θ가 되고 어떤 값이 되는데 이때 y축이 바로 Likelihood가 된다. 그래서 Likelihood가 maximize 되는 곳을 찾는 것이다. θ가 좌우로 움직이면서 y값이 최대가 되는 어떤 지점을 찾을 수 있다. 최대가 되는 지점을 찾으면 그때의 θ는 0.27이라는 것을 알 수 있다. 즉, 우리는 방금 관찰한 관측치(observation)를 가장 잘 설명하는 θ를 찾아내는 과정을 Maximum Likelihood Estimation이라고 한다. 우리가 관찰한 데이터를 가장 잘 설명하는 어떤 확률 분포 함수의 파라미터를 찾아내는 과정.
Optimization
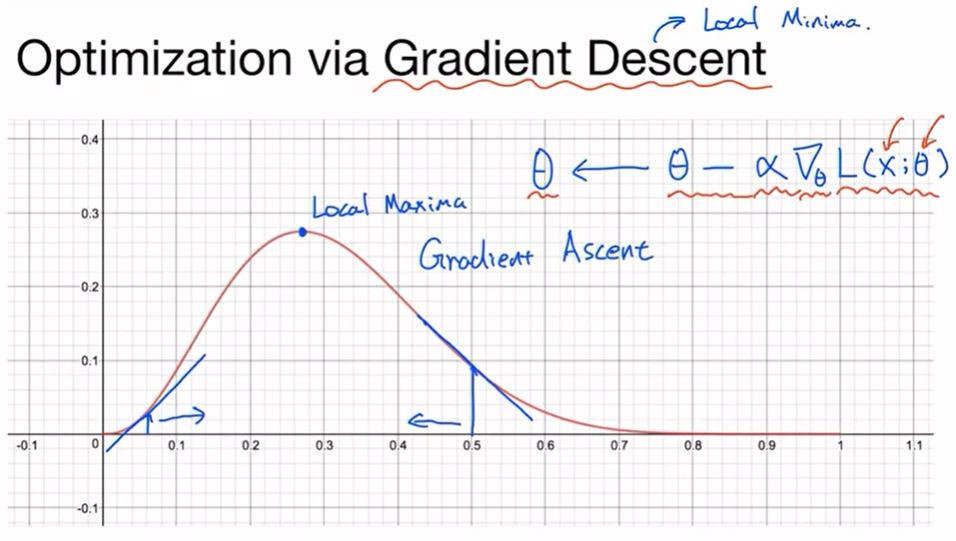
data observation이 잘 관측이 된다면 좋을 것이다. 그래서 observation을 가장 잘 설명하는(수집한 데이터를 가장 잘 설명하는) 확률 분포 함수의 파라미터를 찾는 과정을 거치게 된다. 그렇다면 어떻게 찾을 수 있을까? 바로 그래프의 기울기를 이용한다. 특정 지점에서 시작한다 하면 어느 쪽 방향으로 가야 최대가 되는 지점을 찾을 수 있을지에 따라 이동한다. 지금은 Likelihood를 수행하기 위해서 최대화를 하는 것이고(사실 Gradient Ascent를 수행하는 것), 최대를 찾는 것과 최소를 찾는 것은 다르지 않다. Gradient Descent와 반대로 수행해주기만 하면 된다. Gradient Descent를 기준으로 θ를 업데이트하는 수식은 위의 수식과 같다. 어떤 손실 함수의 값 θ가 주어졌을 때 그리고 데이터 x가 주어졌을 때, 손실 함수(L)의 값을 θ에 대해 미분한 것에 learning rate를 곱해준 것을 기존 θ에서 빼준다. 이것이 바로 Gradient Descent가 된다. 그래서 최대가 되는 Local Maxima(또는 Gradient Descent 일 때는 Local Minima)를 찾는 것이 된다.
Overfitting
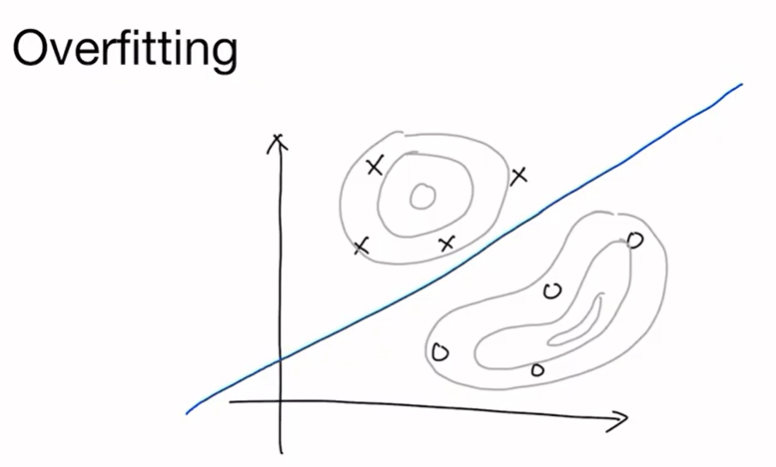
최적화(Gradient Descent를 통해서 손실 값을 minimize 하거나 objective function을 maximize 하는 Gradient Ascent를 통해서)를 통해 주어진 데이터를 가장 잘 설명하는 파라미터 θ를 찾을 수 있다. 하지만 이 Maximum Likelihood Estimation 같은 경우에는 숙명적으로 overfitting이 따르게 된다. 위의 그림과 같이 classification 해야 하는 상황이 주어질 때(O와 X를 가르는 선을 찾고 싶을 때) 최적의 선은 위의 파란색 선과 같을 것이다.
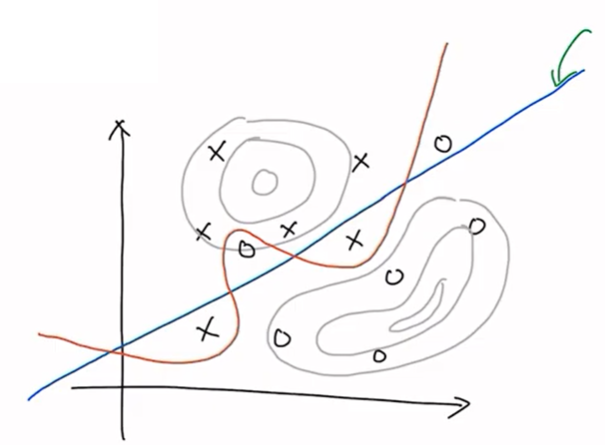
하지만 만약에 데이터 수집이 잘못되어 데이터 분포가 위의 그림과 같고 이것에 대해 훈련한다면 Maximum Likelihood Estimation의 결과는 위와 같이 빨간색 선으로 그어질 것이다. 주어진 데이터에 대해서 과도하게(실제 알고 싶은 decision boundary 파란색이 아닌) fitting 된 상황을 overfitting이라고 한다. 주어진 데이터에 대해서 그 데이터를 가장 잘 설명하는 확률 분포 함수를 찾다 보니 당연히 overfitting이 일어날 수밖에 없다. 따라서 overfitting을 최소화하는 것이 매우 중요하다.
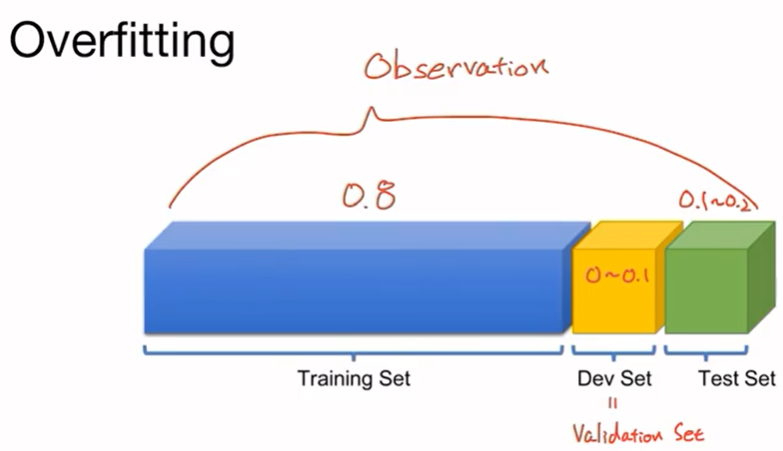
훈련 셋과 테스트 셋을 나누어서 훈련 후에 실제 해당 훈련이 얼마나 잘 학습되었는지 검증하는 방법이다. 예를 들어 수집한 observation(전체 데이터)에 대해서 특정 비율대로 training set, test set, 한발 더 나아가 dev set을 나누어 사용하게 된다. training set은 보통 0.8 정도를 사용하고 test set은 0.1~0.2 정도를 사용하고 dev set은 사용하지 않거나 0.1 정도를 사용한다. test set은 모델이 training set에 Maximum Likelihood Estimation을 통해서 과도하게 학습될 경우 test set에서는 좋은 성능을 내지 못할 것이라는 가정으로, test set을 통해 overfitting이 되었는지 아닌지를 판별할 수 있다. 더 나아가서 test set에 대해서도 overfitting이 될 수 있는데 이를 방지하기 위해 dev set을 사용한다. 딥 러닝 모델을 훈련한다고 가정할 때 training set에 대해 훈련하고 test set에 대해서 검증을 하여 test set에서 가장 좋은 성능을 가진 모델을 선택하도록 작업을 반복한다면 결국에는 training set과 test set에 모두 overfitting 되는 효과를 가져올 수 있다. 따라서 training set을 통해 훈련하고 dev set(또는 validation set)에 대해 검증을 한 후 test set에 test를 하면 훨씬 더 정확한 성능을 얻을 수 있다(이것은 상황에 따라 다르며 dev set과 test set을 동일하게 하나로 사용하기도 함).
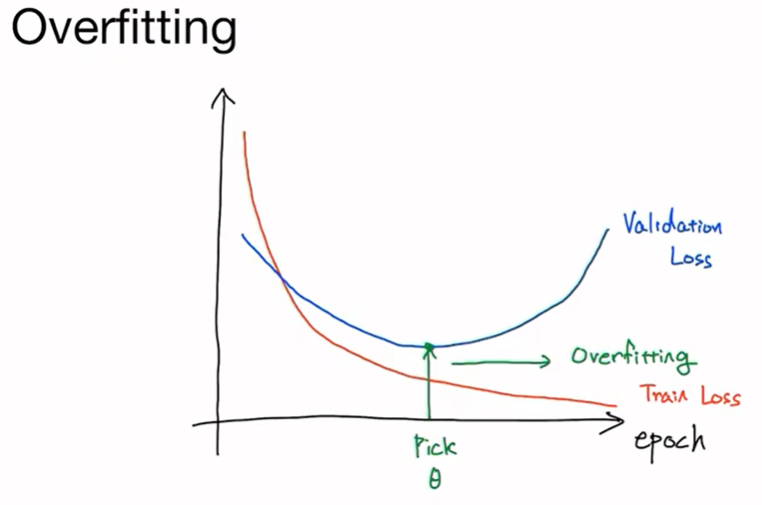
training set을 사용해서 훈련을 하게 되면 epoch이 갈수록 training loss가 떨어지는 것을 볼 수 있다. 이것이 training set에 대한 손실 값이 되고 Maximum Likelihood Estimation을 통해서 training set에 대해서 최대한 잘 설명할 수 있는 확률 분포 함수의 파라미터를 찾도록 되어있기 때문에 loss값은 계속 떨어질 것이다. loss값을 최소로 하는 최적화를 수행하고 있기 때문이다.
validation set이 있고 validation set에 대한 loss를 출력해보면 그림과 같은 현상이 발생하는 것을 볼 수 있다. 어느 순간 validation loss는 올라가기 시작하고 training loss는 계속해서 떨어져서 두 loss 간의 거리가 점점 커지는 것을 볼 수 있다. 이 지점을 overfitting이 되고 있다고 볼 수 있다. 이렇게 training set과 validation set(혹은 test set)을 통해서 현재 모델이 얼마나 overfitting이 되었는가 아니면 얼마나 학습이 진행되었는가를 쉽게 알아볼 수 있고, 또한 validation loss가 커지기 시작하면 훈련을 중단시킬 수 도 있다. 훈련을 중단시키지 않더라도 validation loss가 가장 작은 지점을 선택해야 한다.
이외에도 Overfitting을 막기 위한 여러 방법들이 있다.
1. More Data
- 데이터를 적게 모을수록 실제 분포에서 편향된 분포를 얻을 가능성이 높다. 즉, 데이터를 많이 사용할수록 실제 분포에 가까운 모델을 얻을 수 있다.
2. Less features
- feature를 적게 사용하는 것이 중요하다. feature란 어떤 데이터 분포를 잘 설명하는 특징이다. 예를 들어 사람의 얼굴을 설명할 때, 친구는 안경을 썼고 코가 어떻고 등을 설명할 수 있다. 이와 같이 여러 feature들이 주어지는데 feature들의 숫자를 줄이게 되면 overfitting을 막을 수 있다.
3. Regularization
- Regularization은 다양한 방법들이 있다.
1) Early Stopping
- validation loss가 더 이상 낮아지지 않을 때, 학습을 중단함으로써 overfitting을 방지할 수 있다.
2) Reducing Network size
- deep learning에 한해서 neural network의 사이즈를 줄임으로써 학습해야 하는 양을 줄이는 것도 좋은 방법이 될 수 있다.
3) Weight Decay
- neural network weight 파라미터의 크기를 제한하는 방법이 있음.
4) Dropout
5) Batch Normalization
4), 5)는 neural network에서 많이 사용하는 방법으로 추후 Lab 09에서 다시 다룬다.
Regularization을 통해 overfitting을 방지할 수 있다. 즉, 주어진 데이터를 잘 설명하는 확률 분포 함수의 파라미터를 찾을 수 있지만 주어진 데이터에 대해 너무 과도하게 설명하는 것을 방지하는 것.

Deep Neural Network를 학습할 때 일반적으로 다음과 같은 과정을 거치게 된다.
Practice
필요한 라이브러리들을 import 한다.

x_train은 m개의 sample이 각각 3개의 element를 갖는 1D vector가 된다. y_train을 살펴보면 one-hot 벡터의 index들을 m개 가지고 있는 classification문제임을 알 수 있다. x_text는 (m', 3)의 사이즈 y_test는 (m', ) 개의 one-hot 벡터 index를 가져야 한다.
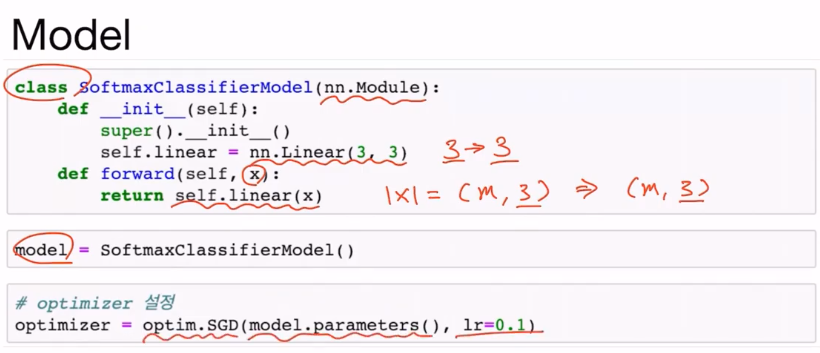
클래스 안에는 하나의 linear layer만 갖으며 3개의 element를 가진 1D 벡터를 입력받아 3개의 element를 가진 1D 벡터를 리턴해준다. self.linear의 리턴은 |x| = (m, 3)의 형태를 갖게 될 것이다.
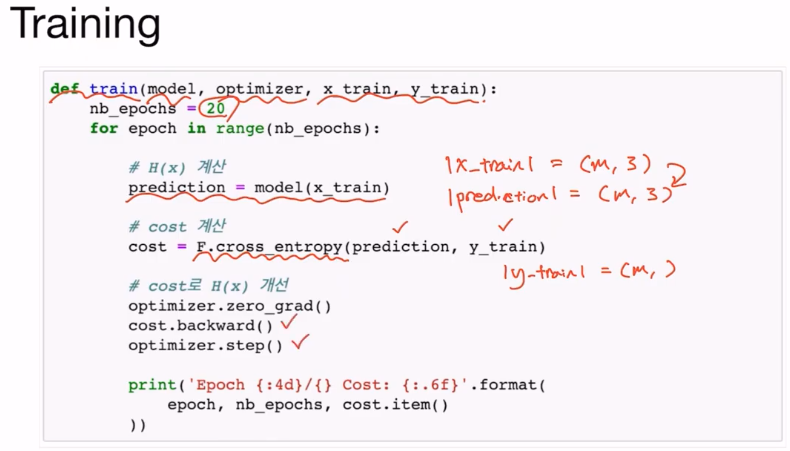
x_train은 m개의 샘플, 3개의 element 크기를 갖고 yprediction은 m개의 샘플, m개의 element 크기(class의 개수)를 갖는다.
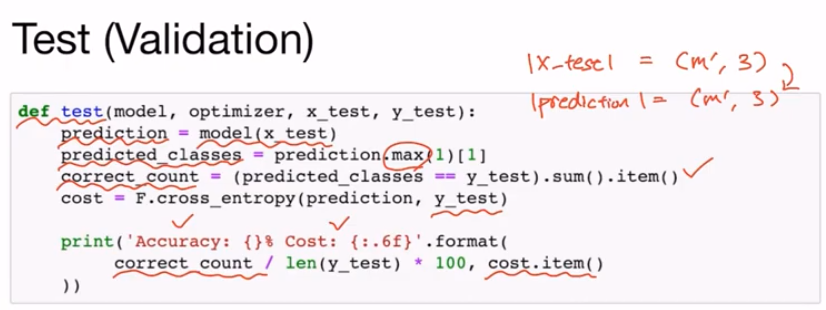
모델을 Test 하는 함수는 다음과 같이 작성할 수 있다.

epoch이 지나갈수록 Maximum likelihood estimation을 통해서 loss값이 점점 떨어져 최적화가 되는 것을 볼 수 있다. 즉, x_train과 y_train을 잘 설명하는 neural network의 파라미터가 optimizer를 통해 찾아지고 있는 것. 그런데, test 함수를 수행해서 그 결과를 살펴보면 cost가 증가한 것을 볼 수 있다. 이것은 train loss는 계속 떨어지고 있지만, test loss가 이미 올라가버린 overfitting 상황이 발생했을 것이라 추측할 수 있다.
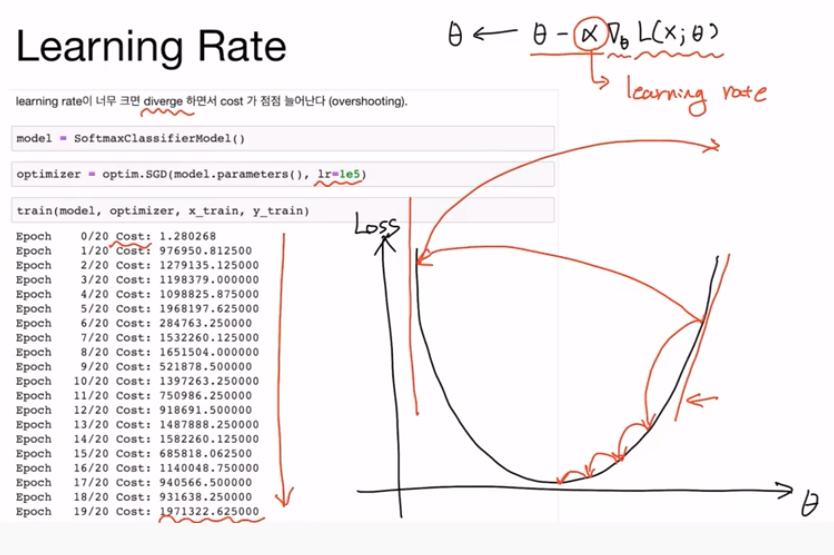
loss 함수의 값을 최소로 하는 방향으로 Θ를 업데이트하는데, 이때 α가 바로 learning late이다. 즉, 학습 속도를 조절할 수 있다. learning late가 너무 크면 발산(diverge) 하는 경우가 발생한다.
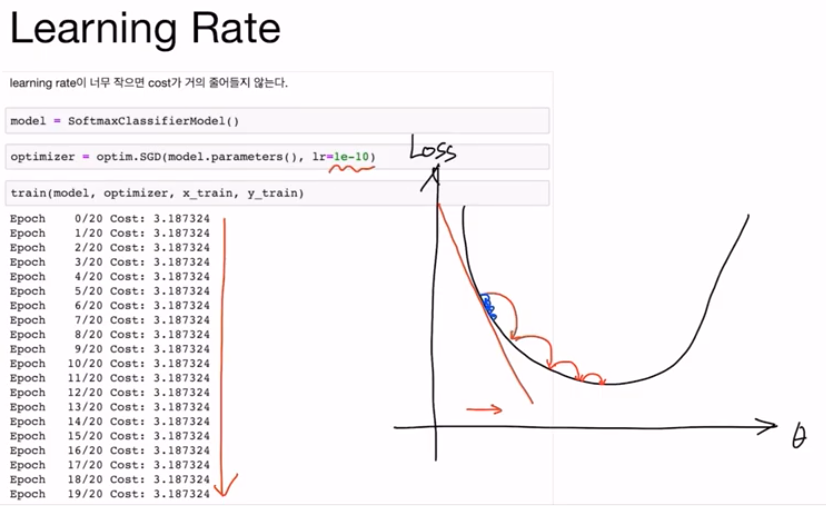
반대로 learning late가 너무 작아도 문제가 된다. learning late가 너무 작으면 학습을 진행하더라도 원하는 방향으로는 움직이겠지만 이동이 적어 학습이 진행되지 않을 수 있다. 따라서 모델을 학습시킬 때 learning late를 잘 설정하는 것이 중요한데, 정해진 것은 없고 경험적으로 적절한 숫자로 조절할 필요가 있다.


데이터가 주어졌을 때 학습하기 쉽도록 미리 바꿔주는 것은 매우 중요하다. 위의 경우 y_train의 값을 보면 regressiong 문제임을 알 수 있다. 이때는 MSE를 통해 loss를 계산할 수 있다.

이때 데이터 전처리를 적용하면 학습이 한층 수월해진다. 여기서 사용한 방법은 정규분포화(Standardization)이다. 정규분포를 따르는(0~1) training set을 만들 수 있다.



만약 전처리를 수행하지 않았다면 최적화에 어려움이 있었을 것이다. 만약 y_train이 2개의 element를 갖는 상황에서 첫 번째 칼럼은 매우 큰 값을 갖고 두 번째 칼럼은 매우 작은 값을 갖고 학습을 수행하면 모델은 큰 값(첫 번째 칼럼)에만 집중을 하게 될 것이다. 하지만 전처리를 수행한다면 적당한 범위의 값으로 변환이 되고 neural network는 수월하게 학습을 진행할 수 있을 것이다.
'머신러닝(machine learning)' 카테고리의 다른 글
| [Pytorch] 08-1 Perceptron (1) | 2022.01.14 |
|---|---|
| [Pytorch] 07-2 MNIST Introduction (0) | 2022.01.14 |
| [Pytorch] 06-2 Softmax Classification Pytorch (0) | 2021.12.29 |
| [Pytorch] 06-1 Softmax Classification (0) | 2021.12.28 |
| [Pytorch] 05-2 Logistic Regression 2 (0) | 2021.12.23 |




