| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 머신러닝
- BAEKJOON
- DP
- MSE
- AI
- 홍콩과기대김성훈교수
- pytorch
- 스택
- tensorflow
- 백준
- DynamicProgramming
- 강의정리
- 파이토치
- 알고리즘
- 머신러닝 기초
- Deep learning
- 정렬
- rnn
- 자연어처리
- 딥러닝
- machine learning
- Python
- loss
- classifier
- Natural Language Processing with PyTorch
- 강의자료
- Softmax
- Hypothesis
- Cross entropy
- 파이썬
- Today
- Total
개발자의시작
[Pytorch] 04-1 Multivariate Linear Regression 본문
이 글은 모두를위한딥러닝 시즌2 https://github.com/deeplearningzerotoall/PyTorch 을 정리한 글입니다.
GitHub - deeplearningzerotoall/PyTorch: Deep Learning Zero to All - Pytorch
Deep Learning Zero to All - Pytorch. Contribute to deeplearningzerotoall/PyTorch development by creating an account on GitHub.
github.com
Multivariate Linear regression
- 여러 개의 정보로부터 하나의 추측 값을 계산하는 모델
복수의 정보를 가지고 어떻게 예측을 할 수 있을까?

Data
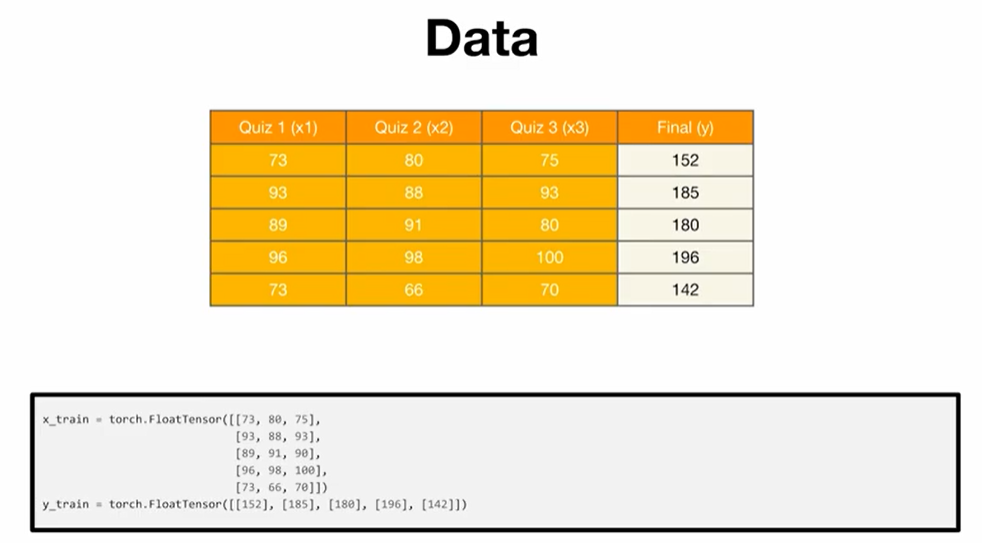
Hypothesis Function
- hypothesis 는 다음과 같이 나타낼 수 있다.

하지만, x의 길이가 일일이 지정해 줄 수 없을 만큼 길다면?

Cost Function 역시 simple Linear Regression과 동일한 공식을 갖는다.

학습방식 역시 동일하다.

Full Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train.matmul(W) + b # or .mm or @
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
))
|
simple linear regression과 달라지는 부분은 데이터 정의와 모델 정의뿐이다. 특히, 학습하는 부분(for 문)이 동일한 것은 Pytorch의 확장성을 잘 보여주는 예이다.
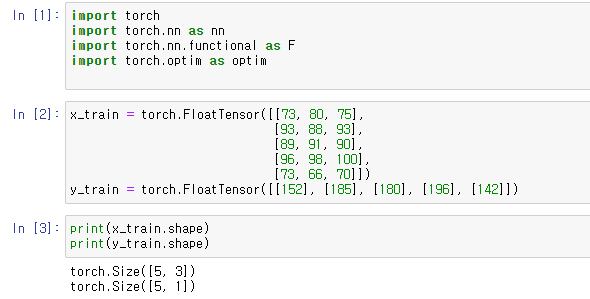

cost는 점점 작아지고 y에 점점 가까워지는 H(x)를 볼 수 있다. 학습시 Learning rate에 따라 발산할 수 도 있다.
- detach()는 기존 텐서에서 gradient 전파가 안되는 텐서를 생성하는 함수
Multivariate linear regression을 구현할때 W를 일일이 구현하는 것은 매우 비효율적이다.
- PyTorch에서는 nn.Module이라는 효율적인 모듈을 제공한다.

또한, PyTorch는 다양한 cost function을 제공한다.
- cost function은 한줄이면 되는데 굳이 왜 사용하냐고 생각할 수 있지만, 후에 다른 cost function을 사용할 때 변경하기도 용이하고 cost function을 계산할 때 발생할 수 있는 버그가 없어 디버깅 시 용이하기도 하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1)
def forward(self, x):
return self.linear(x)
# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 모델 초기화
model = MultivariateLinearRegressionModel()
# 병경 포인트 1
#W = torch.zeros((3, 1), requires_grad=True)
#b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# 변경 포인트2
#hypothesis = x_train.matmul(W) + b # or .mm or @
# cost 계산
cost = F.mse_loss(prediction, y_train)
# 변경 포인트3
#cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
|
※ 변경된 부분!
1. 모델 정의 -> model = MultivariateLinearRegressionModel()
2. hypothesis 계산 -> prediction = model(x_train)
3. Gradient descent -> cost = F.mse_loss(prediction, y_train)
'머신러닝(machine learning)' 카테고리의 다른 글
| [Pytorch] 05-1 Logistic Regression (0) | 2021.12.08 |
|---|---|
| [Pytorch] 04-2 Loading Data (0) | 2021.11.30 |
| [Pytorch] 03 Deeper Look at GD (0) | 2021.11.30 |
| [Pytorch] 02 Linear regression (0) | 2021.11.30 |
| [Pytorch] 01-2 Tensor Manipulation 2 (0) | 2021.11.26 |




