| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 강의정리
- 자연어처리
- DynamicProgramming
- Hypothesis
- Softmax
- DP
- tensorflow
- BAEKJOON
- AI
- classifier
- Deep learning
- 백준
- Natural Language Processing with PyTorch
- Cross entropy
- Python
- rnn
- machine learning
- 파이썬
- MSE
- 정렬
- 스택
- 딥러닝
- loss
- pytorch
- 머신러닝
- 머신러닝 기초
- 알고리즘
- 파이토치
- 홍콩과기대김성훈교수
- 강의자료
- Today
- Total
개발자의시작
[Pytorch] 02 Linear regression 본문
은 모두를위한딥러닝 시즌2 https://github.com/deeplearningzerotoall/PyTorch 을 정리한 글입니다.
이번 챕터에서 모델링하려는 것은 공부시간과 점수의 상관관계이다.

내가 4시간을 공부했다면 몇 점 정도를 받을 수 있을까? 를 예측하는 것이다.
모델의 학습을 위한 데이터는 "torch.tensor"의 형태이며, 입력과 출력을 각기 다른 텐서에 저장한다.
입력은 x_train, 출력은 y_train 로 표기한다.
|
1
2
3
4
5
6
7
|
import torch
import numpy as np
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
print(x_train)
print(y_train)
|

※ Linear Regression은 학습 데이터와 가장 맞는 하나의 직선을 찾는 것!
Hypothesis

|
1
2
3
|
W = torch.zeros(1, requires_grad=True )
b = torch.zeros(1, requires_grad=True )
hypothesis = x_train * W + b
|

Weight 와 Bias를 0으로 초기화한다. -> 처음에 어떤 입력을 받아도 0을 예측.
requires_grad=True -> W와 b를 학습시키는 것이 목적이므로, 두 변수를 학습할 것이라고 명시.
학습을 하기 위해서는 모델이 얼마나 정답과 가까운지 알아야 한다.
정답과 예측의 차이를 cost 또는 loss라고하는데, linear regression에서는 Mean Squared Error(MSE)라는 함수로 loss를 계산한다. MSE라는 loss는 단순히 예측값과 실제 train_y의 차이를 제곱해서 평균을 낸 것이다.
Mean Squared Error
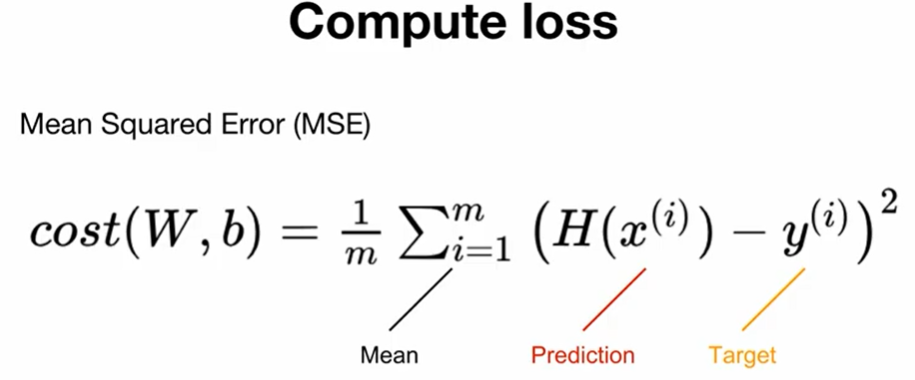
- MSE는 torch.mean() 으로 계산.
- loss를 통해서 모델을 개선할 차례.
- optimizer는 SGD를 사용. ( torch.optim.SGD() )
- 학습할 tensor는 W와 b이므로 이를 리스트로 넣어줌.
- lr(learning rate)는 적당한 값으로 사용.
아래 3줄은 항상 같이 붙어다니는 3줄!
- zero_grad() -> gradient 초기화
- backward() -> gradient 계산
- step() -> 개선
|
1
2
3
4
5
6
7
|
cost = torch.mean((hypothesis - y_train)**2)
optimizer = torch.optim.SGD([W, b], lr= 0.01)
optimizer.zero_grad()
cost.backward()
optimzer.step()
|

Full training code
# 한번만!
1. 데이터 정의
2. Hypothesis 초기화
3. Optimizer 정의
# 반복!
1. Hypothesis 예측
2. Cost 계산
3. Optimizer로 학습
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
##### Full training code #####
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
W = torch.zeros(1, requires_grad=True )
b = torch.zeros(1, requires_grad=True )
hypothesis = x_train * W + b
optimizer = torch.optim.SGD([W, b], lr= 0.01)
nb_epochs= 1000
for epoch in range(1, nb_epochs + 1):
hypothesis = x_train * W + b
cost = torch.mean((hypothesis - y_train)**2)
optimizer.zero_grad()
cost.backward()
optimizer.step()
|
'머신러닝(machine learning)' 카테고리의 다른 글
| [Pytorch] 04-1 Multivariate Linear Regression (0) | 2021.11.30 |
|---|---|
| [Pytorch] 03 Deeper Look at GD (0) | 2021.11.30 |
| [Pytorch] 01-2 Tensor Manipulation 2 (0) | 2021.11.26 |
| [Pytorch] 01-1 Tensor Manipulation 1 (0) | 2021.11.26 |
| 도커[Docker] Instruction (0) | 2021.11.18 |




